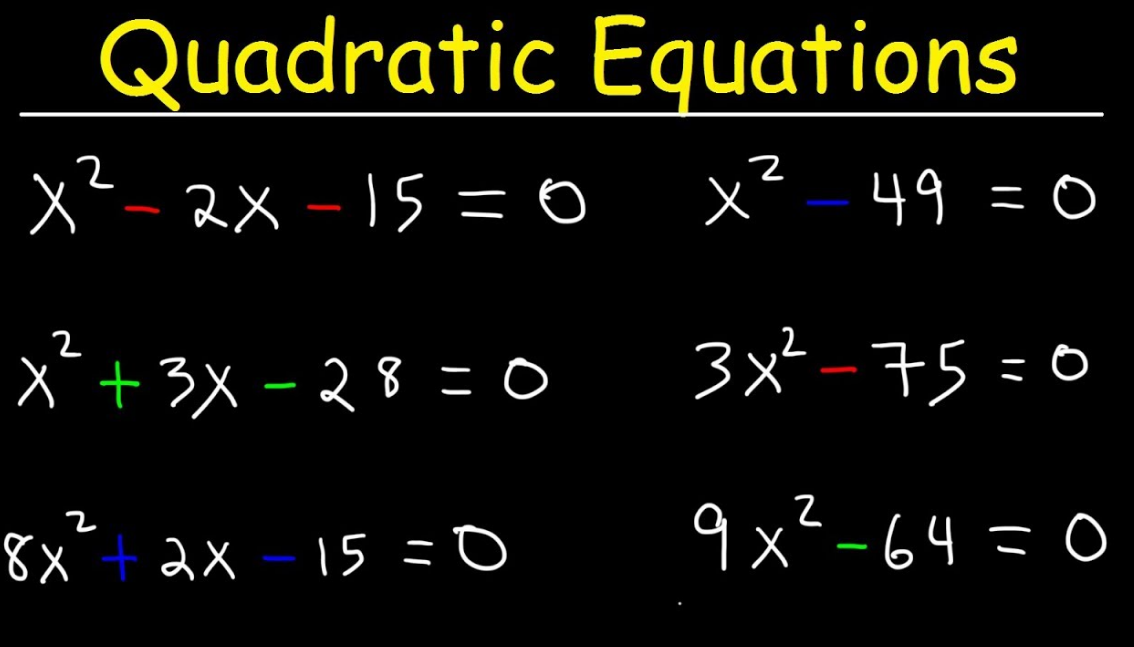Before going to learn about solving quadratic equations, let us recall a few facts about quadratic equations. The word “quadratic” is originated from the word “quad” and its meaning is “square”. It means the quadratic equation has a variable raised to 2 as the greatest power term. The standard form of a quadratic equation is given by the equation ax2 + bx + c = 0, where a ≠ 0. We know that any value(s) of x that satisfies the equation is known as a solution (or) root of the equation and the process of finding the values of x which satisfy the equation ax2 + bx + c = 0 is known as solving quadratic equations.
There are different methods used to solve quadratic equations. But the most popular method is solving quadratic equations by factoring. Let us learn all the methods in detail here along with a few solved examples.
Table of Contents
How to Solve Quadratic Equations?
Solving quadratic equations means finding a value (or) values of the variable which satisfy the equation. The value(s) that satisfy the quadratic equation is known as its roots (or) solutions (or) zeros. Since the degree of the quadratic equation is 2, it can have a maximum of 2 roots. For example, one can easily see that x = 1 and x = 2 satisfy the quadratic equation x2 – 3x + 2 = 0 (you can substitute each of the values in this equation and verify). Thus, x = 1 and x = 2 are the roots of x2 – 3x + 2 = 0. But how to find them if they are not given? There are different ways of solving quadratic equations.
- Solving quadratic equations by factoring
- Solving quadratic equations by completing the square
- Solving quadratic equations by graphing
- Solving quadratic equations by quadratic formula
Apart from these methods, there are some other methods that are used only in specific cases (when the quadratic equation has missing terms) as explained below.
Solving Quadratic Equations Missing b
In a quadratic equation ax2 + bx + c = 0, if the term with b is missing then the equation becomes ax2 + c = 0. This can be solved by taking square root on both sides. The process is explained with examples below.
- x2 – 4 = 0 ⇒ x2 = 4 ⇒ x = ±√4 ⇒ x = ± 2
Thus, the roots of the equation are 2 and -2. - x2 + 36 = 0 ⇒ x2 = -36 ⇒ x = ±√(-36) ⇒ x = ± 6i
Thus, the roots of the equation are 6i and -6i.
(note that these are imaginary (or) complex numbers).
Solving Quadratic Equations Missing c
In a quadratic equation ax2 + bx + c = 0, if the term with c is missing then the equation becomes ax2 + bx = 0. To solve this type of equation, we simply factor x out from the left side, set each of the factors to zero, and solve. The process is explained with examples below.
- x2 – 5x = 0 ⇒ x (x – 5) = 0 ⇒ x = 0; x – 5 = 0 ⇒ x = 0; x = 5
Thus, the roots of the equation are 0 and 5. - x2 + 11x = 0 ⇒ x (x + 11) = 0 ⇒ x = 0; x + 11 = 0 ⇒ x = 0; x = -11
Thus, the roots of the equation are 0 and -11.
Now, we will learn the methods of solving the quadratic equations in each of the above-mentioned methods.
Solving Quadratic Equations by Factoring
Solving quadratic equations by factoring is one of the famous methods used to solve quadratic equations. The step-by-step process of solving quadratic equations by factoring is explained along with an example where we will solve the equation x2 – 3x + 2 = 0.
- Step – 1: Get the equation into standard form. i.e., Get all the terms of to one side (usually to left side) of the equation such that the other side is 0.
The equation x2 – 3x + 2 = 0 is already in standard form. - Step – 2: Factor the quadratic expression. If you want to know how to factor a quadratic expression, click here.
Then we get (x – 1) (x – 2) = 0. - Step – 3: By zero product property, set each of the factors to zero.
x – 1 = 0 (or) x – 2 = 0 - Step – 4: Solve each of the above equations.
x = 1 (or) x = 2
Thus, the solutions of the quadratic equation x2 – 3x + 2 = 0 are 1 and 2. This method is applicable only when the quadratic expression is factorable. If it is NOT factorable, then we can use one of the other methods as explained below. Similar to quadratic equations we have solutions for linear equations, which are used to solve linear programming problems.
Solving Quadratic Equations by Completing Square
Completing the square means writing the quadratic expression ax2 + bx + c into the form a (x – h)2 + k (which is also known as vertex form), where h = -b/2a and ‘k’ can be obtained by substituting x = h in ax2 + bx + c. The step-by-step process of solving the quadratic equations by completing the square is explained along with an example where we are going to find the solutions of the equation 2x2 + 8x = -3.
- Step – 1: Get the equation into standard form.
Adding 3 on both sides, we get 2x2 + 8x + 3 = 0. - Step – 2: Complete the square on the left side.
Then we get 2 (x + 2)2 – 5 = 0. If you want to know how to complete the square. - Step – 3: Solve it for x (We will have to take square root on both sides along the way).
Adding 5 on both sides,
2 (x + 2)2 = 5
Dividing both sides by 2,
(x + 2)2 = 5/2
Taking square root on both sides,
x + 2 = √(5/2) = √5/√2 · √2/√2 = √10/2
Subtracting 2 from both sides,
x = -2 ± (√10/2) = (-4 ± √10) / 2
Thus, the roots of the quadratic equation 2x2 + 8x = -3 are (-4 + √10)/2 and (-4 – √10)/2.
Solving Quadratic Equations by Graphing
For solving the quadratic equations by graphing, we first have to graph the quadratic expression (when the equation is in the standard form) either manually or by using a graphing calculator. Then the x-intercept(s) of the graph (the point(s) where the graph cuts the x-axis) are nothing but the roots of the quadratic equation. Here are the steps to solve quadratic equations by graphing which are explained along with an example where we are going to solve the equation 3x2 + 5 = 11x.
- Step – 1: Get into the standard form.
Subtracting 11x from both sides, 3x2 – 11x + 5 = 0. - Step – 2: Graph the quadratic expression (which is on the left side).
Graph the quadratic function y = 3x2 – 11x + 5 either manually or using a graphing calculator (GDC).
You can see the graph in the step below. - Step – 3: Identify the x-intercepts.
- Step – 4: The x-coordinates of the x-intercepts are nothing but the roots of the quadratic equation.
Thus, the solutions of the quadratic equation 3x2 + 5 = 11x are 0.532 and 3.135.
By seeing the above example, we can see that the graphing method of solving quadratic equations may not give the exact solutions (i.e., it gives only the decimal approximations of the roots if they are irrational). i.e., if we solve the same equation using completing the square, we get x = (11 + √61) / 6 and x = (11 – √61) / 6. But we cannot get these exact roots by the graphing method.
What if the graph does not intersect the x-axis at all? It means that the quadratic equation has two complex roots. i.e., the graphing method is NOT helpful to find the roots if they are complex numbers. We can use the quadratic formula (which is explained in the next section) to find any type of roots.
Solving Quadratic Equations by Quadratic Formula
As we have already seen, the previous methods for solving the quadratic equations have some limitations such as the factoring method is useful only when the quadratic expression is factorable, the graphing method is useful only when the quadratic equation has real roots, etc. But solving quadratic equations by quadratic formula overcomes all these limitations and is useful to solve any type of quadratic equation. Here is the step-by-step explanation of solving quadratic equations by quadratic formula along with an example where we will be finding the solutions of the quadratic equation 2x2 = 3x – 5.
- Step – 1: Get into the standard form.
Then the above equation becomes 2x2 – 3x + 5 = 0. - Step – 2: Compare the equation with ax2 + bx + c = 0 and find the values of a, b, and c.
Then we get a = 2, b = -3. and c = 5. - Step – 3: Substitute the values into the quadratic formula which says x = [-b ± √(b² – 4ac)] / (2a). Then we get
x = [-(-3) ± √((-3)² – 4(2)(5))] / (2(2)) - Step – 4: Simplify.
x = [ 3 ± √(9 – 40) ] / 4
= [ 3 ± √(-31) ] / 4
= [ 3 ± i√(31) ] / 4
Thus, the roots of the quadratic equation 2x2 = 3x – 5 are [ 3 + i√(31) ] / 4 and [ 3 – i√(31) ] / 4. In the quardratic formula, the expression b² – 4ac is called the discriminant (that is denoted by D). i.e., D = b² – 4ac. This is used to determine the nature of roots of the quadratic equation.
Nature of Roots Using Discriminant
- If D > 0, then the equation ax2 + bx + c = 0 has two real and distinct roots.
- If D = 0, then the equation ax2 + bx + c = 0 has only one real root.
- If D < 0, then the equation ax2 + bx + c = 0 has two distinct complex roots.
Thus, using the discriminant, we can find the number of solutions of quadratic equations without actually solving it.
Important Notes on Solving Quadratic Equations:
- The factoring method cannot be applied when the quadratic expression is NOT factorable.
- The graphing method cannot give the complex roots and also it cannot give the exact roots in case the quadratic equation has irrational roots.
- Completing the square method and quadratic formula method can be applied to solve any type of quadratic equation.
- The roots of the quadratic equation are also known as “solutions” or “zeros”.
- For any quadratic equation ax2 + bx + c = 0,
the sum of the roots = -b/a
the product of the roots = c/a.