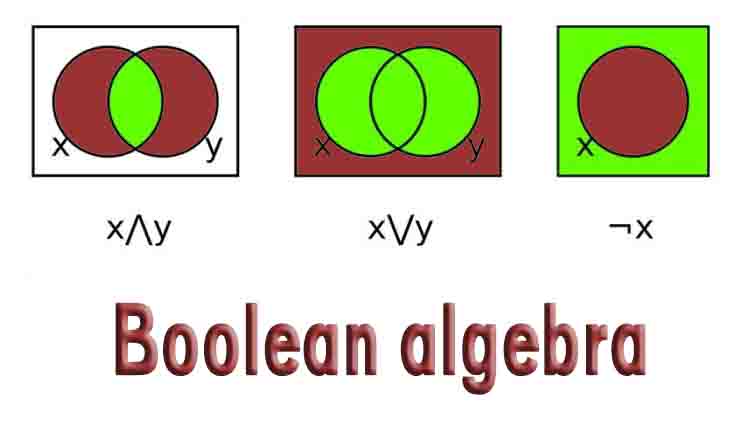
Boolean algebra is a branch of algebra. Used for dealing with logical expressions, which are composed of variables, logical operators, and constants. In Boolean algebra, variables take only two values, it is represented as 1 or 0, False or true, and off or on.
AND, OR, and NOT are the fundamental logical operators in Boolean algebra. If both values are true, the AND operation returns the true value. If anyone from a given value is true, the OR operation returns the True value. The NOT operator returns the opposite of its given values, for example, if the input value is true the result is false.
The Boolean algebra also includes additional logical operators, such as NAND (not-and), NOR(not-or), and XOR (exclusive or), among others.
In this article we will discuss the definition of Boolean algebra, the operation of Boolean algebra, laws of Boolean algebra, and also with the help of an example topic will be explained.
Table of Contents
Define Boolean Algebra
Boolean algebra is a part of algebra that deals with the mathematical operations and law governing logical expressions composed of variables, logical operators, and constants.
The rules and laws of Boolean algebra define how logical expressions can be simplified, manipulated, and transformed into equivalent expressions. Boolean provides a formal mathematical framework for designing and analyzing digital circuits, programming languages, and software systems. It is also used in various fields, including electrical engineering, computer science, and mathematics.
Process of Boolean Algebra
The basic operation or process of Boolean algebra are:
- AND or Conjunction operation
- OR operation or Disjunction
- Not operation or Negation
Some basic operations of Boolean algebra discussed below in the table
| Operator | Symbol | Precedence |
| AND | . (or) ∧ | Middle |
| NOT | ‘ (or) ¬. | Highest |
| OR | + (or) ∨ | Lowest |
With the help of these operations, we can solve in Boolean algebra easily.
Boolean algebra Laws
For dealing with logic operations and binary variables Boolean algebra can be used. Boolean algebra has many rules that are used for logical expressions. Here we discussed some basic fundamental rules:
Commutative Law
The commutative law changes only the order of operands in an operation not changes the result of a given operation.
a. A ∧ B = B ∧ A
b. A ∨ B = B ∨ A
Associative Law
The associative law states that the grouping of operands in an operation does not affect the result.
a. (A ∧ B) ∧ C = A ∧ (B ∧ C)
b. (A ∨ B) ∨ C = A ∨ (B ∨ C)
For example, (A ∨ B) ∨ C = A ∨ (B ∨ C) and (A ∧ B) ∧ C = A ∧ (B ∧ C).
Distributive Law
The distributive law states that the product of two terms added to a third term is equal to the sum of the product of the first term and the third term and the product of the second term and the third term.
a. A ∧ (B ∨ D) = (A ∧ B) ∨ (A ∧ D)
b. A ∨ (B ∧ D) = (A ∨ B) ∧ (A ∨ D)
Identity Law
The identity law states that the result of an operation with one operand and a logical value is the operand itself.
a. A ∧ 1 = A
b. A ∨ 0 = A
Negation Law
The negation law states that the negation of operand results in the opposite logical value.
- A ∧ ¬A = 0
- A ∨ ¬A = 1
Double Negation Law
The double negation law states that negating an operand twice is equivalent to the operand itself.
- ¬(¬A) = A.
De Morgan’s Law
De Morgan’s law states that the negation of a conjunction (AND) is the disjunction (OR) of the negations of the operands, and the negation of a disjunction (OR) is the conjunction (AND) of the negations of the operands.
a. ¬(A ∧ B) = ¬A ∨ ¬B
b. ¬(A ∨ B) = ¬A ∧ ¬B
These rules can be used to simplify and transform logical expressions to their simplest form.
Examples of Boolean algebra
Example 1:
Draw the truth table for A(B+C)
Solution
| A | B | C | B+C | A(B+C) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Example 2:
Simplify the given question
D+B̅D̅
Solution:
Given
D + B̅D̅ (1)
According to De Morgan’s law
D + (B̅ + D̅)
For commutative law
(D + D̅) + B̅
Again apply commutative law
1 + B̅=1
Therefore, equation one is
D + B̅D̅= 1 Answer
The above problem of the Boolean algebra can also be solved with the help of a Boolean calculator to avoid confusing calculations by using laws.
Frequently Asked Question
Question no 1:
What is the meaning of Boolean algebra?
Answer
Boolean algebra is a branch of algebra that deals with binary variables and binary operations. It is named after George Boole, a mid-19th century mathematician who first introduced the concept of Boolean algebra in the. In Boolean algebra, the variables take on one of two values, typically 0 or 1, and the operations involve logical operations such as AND, OR, and NOT.
Question 2:
What is a truth table in Boolean algebra?
Answer:
The truth table lists all possible combinations of input values and the corresponding output values for the expression. Truth tables are useful for evaluating and simplifying Boolean expressions.
Question 3:
What is a Boolean function?
Answer:
A Boolean function is a mathematical function that operates on binary variables and produces a binary output. It is typically expressed in terms of Boolean algebraic operations such as AND, OR, and NOT. Boolean functions are used in digital logic circuits, computer science, and other fields where binary logic is important.
Question 4:
What is a logic gate in Boolean algebra?
Answer:
A logic gate is an electronic circuit that performs a Boolean function. It takes one or more binary inputs and produces a binary output based on a predefined Boolean function. Logic gates are the building blocks of digital logic circuits, such as computer processors and memory chips.
Summary
In this article, we have discussed the definition of Boolean algebra, the operation of Boolean algebra, laws of the Boolean algebra, and also discussed some basic examples. After studying this article anyone can defend this topic easily.