How to Find the Range of a Function? Mathematical functions can be compared to vending machines. They give back some cookies or cans in exchange for the money they receive. Similarly, functions take numbers as inputs and return results as outputs. The reality is that everything in real life can be formulated and solved with the help of functions.
Almost everything in real life has a mathematical model, from building design to architecture to Mega Skyscrapers. Because of this, we cannot ignore the importance of functions in our lives. The Domain and Range of a function are two parameters to describe it.
For instance, the machine may indicate that only notes of Rs.20 and Rs.50 can be used to purchase items. What if someone uses Rs.10 notes? The machine will not give any output. Therefore, the domain of a function represents the possible inputs available.
Specifically, Rs.20 and Rs.50 notes are the domain of the “Vending Machine”. The sandwich machine will not produce sandwiches regardless of how much money is put in it. This is where the concept of range comes into play. The range is the possible outputs a machine can give.
Table of Contents
Range and Domain of a Function
Domain of a Function:
For a function to produce valid results, it must have all the input values that it can take. Inputs are the possible values that a function can take.
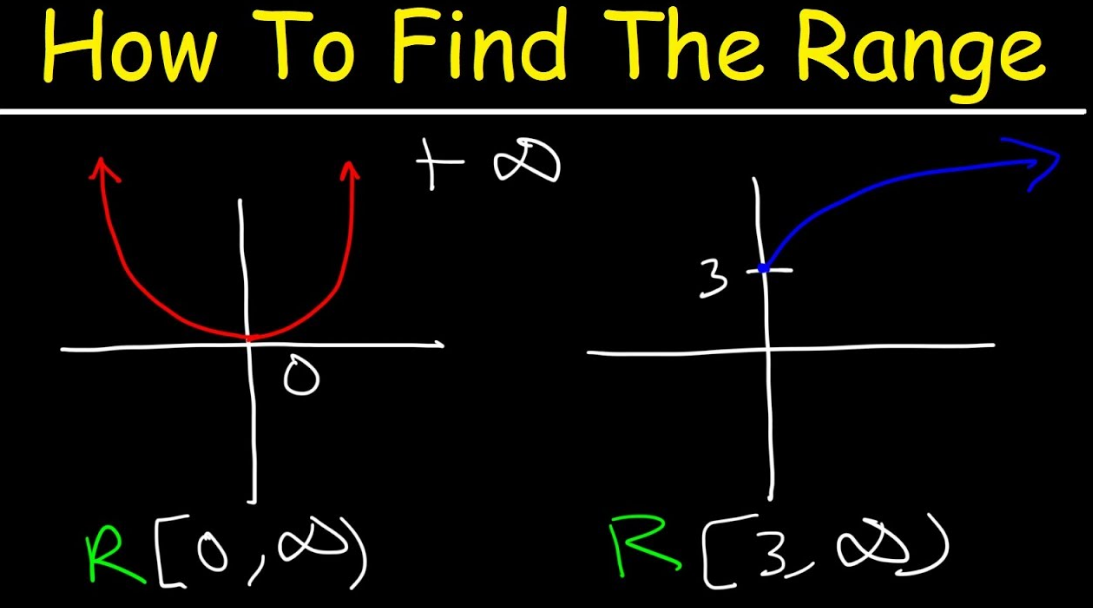
For example: In the figure below, f(x) = x2. The set of all inputs is called the domain, and the set of all outputs is called the range.
Algebraically, there are various ways to find the range of a function. However, before we get to that, let’s briefly go over the Range of a Function.
In the first chapter What is a Function? , we learned that a function is expressed as
y=f(x)y=f(x),
X and Y are the inputs and outputs, respectively.
For every input x (where f(x) is defined), there is a unique output.
Range of a Function represents all outputs of a function.
Range of a function is the set of all y values or outputs, i.e., the set of all f(x)f(x) when it is defined.
Steps to Find the Range of a Function
Let’s consider finding the range of a function such as f(x)=x+2f(x)=x+2.
We can find the range of a function by following these steps:
First label the function as y=f(x)
y=x+2y=x+2
Express x as a function of y
Here x=y-2x=y−2
Find all possible values of y for which f(y) can be defined
See that x=y-2x=y−2 is defined for all real values of yy.
By looking at f(x), we can determine the elements of y
Our initial function y=x+2y=x+2 is defined for all real values of xx i.e., x\epsilon \mathbb{R}xϵR.
So here we do not need to eliminate any value of yy i.e., y\epsilon \mathbb{R}yϵR.
Write the range of the function f(x)
Therefore the Range of the function y=x+2y=x+2 is {y\epsilon \mathbb{R}yϵR}.
Perhaps you are getting confused now and don’t understand all the steps.
Nevertheless, you will get a clear understanding of the concept in the following examples.