In order to find the integral of sin x, let us first review what integral means. In the math world, the term integral refers to the antiderivative. Antiderivatives, as their name suggests, come about by reversing differentiation. i.e.,
- Finding f'(x) from f(x) is differentiation.
- Finding f(x) from f'(x) is integration.
By using differentiation, we can find the integration of sin x. Here is the formula, proof, and graphical intuition of sin x, along with the integral of sin x.
Table of Contents
What is the Integral of Sin x?
The integral of sin x is -cos x. From a mathematical perspective, there is the following expression: * sin x dx = -cos x + C, where C represents the integration constant. Here,
- ‘∫’ represents the “integral.”
- Sin x is the integrand
- dx is always associated with any integral and represents the slight difference in angle x.
However, how do we solve the integration of sin x? We can do this in various methods, such as using derivatives and using the substitution method. In the upcoming sections, we will see how each of these methods proves the integral of sin x.
Integral of Sin x Formula
A sine x integral is a cosine x integral. i.e.,
- ∫ sin x dx = -cos x + C, where C is the constant of integration.
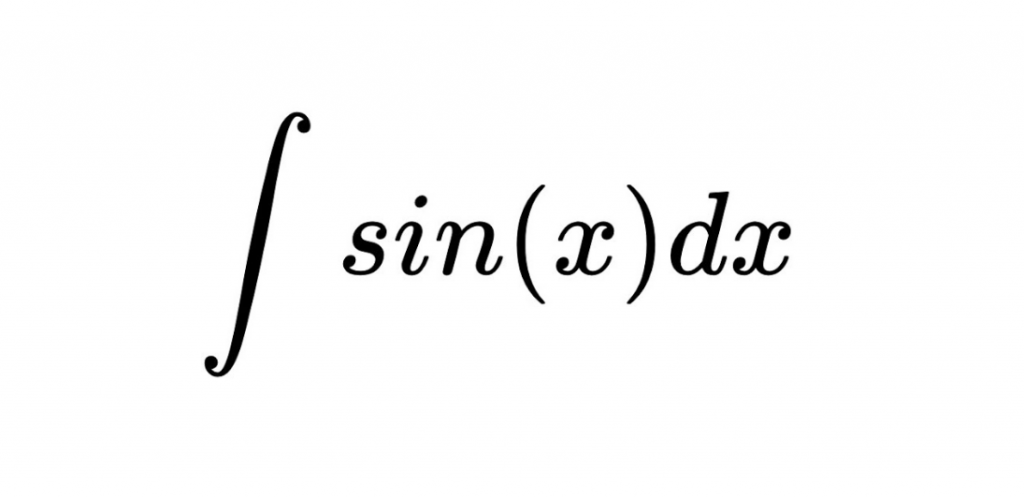
Integral of Sin x Proof by Derivatives
Integration is the opposite process of differentiation. To find the integral of sin x, we must differentiate the function that gives us sin x. i.e., we have to see
d/dx ?? = sin x.
Remember what we learned about differentiation formulas, and we’ll look for a formula that gives us the derivative sin x. It’s true that there is a formula which states d/dx (cos x) = -sin x. Whoops! This gives -sin x, but we wanted it to be sin x. No worries! Let’s multiply both sides by -1 to get what we want. Then we get
-d/dx (cos x) = – (-sin x) (or)
d/dx (-cos x ) = sin x
Thus, -cos x is the derivative of sin x. Hence, sinx (antiderivative) must be integrated as – cosx. However, integration constants are always added before integration. Thus, we have
∫ sin x dx = -cos x + C
Hence proved.
Substitution method for proof of Sinx integral
We can prove that the integral of sin x is -cos x + C using the substitution method. Y is assumed to equal sin x in this case. Then DY/DX = = cos x (or)
dy = cos x dx
According to trigonometric identities, cos x = √1 – sin²x. Then the above equation becomes,
dy = √1 – sin²x dx
dy = √1 – y² dx
dy / √1 – y² = dx
Multiplying both sides by sin x,
(sin x dy) / √1 – y² = sin x dx
On the left side, substitute sin x = y.
(y dy) / √1 – y² = sin x dx
Integrating on both sides,
∫ (y dy) / √1 – y² = ∫ sin x dx
Let 1 – y² = u. Then -2y dy = du (or) y dy = -1/2 du.
Then the above left-hand side integral becomes,
(-1/2) ∫ 1/√u du = ∫ sin x dx
(-1/2) ∫ u-1/2 du = ∫ sin x dx
According to the integration formula, ∫ xn dx = (xn+1)/(n+1) + C. So we get
(-1/2) (u1/2 / (1/2)) + C = ∫ sin x dx
-u1/2 + C = ∫ sin x dx
Substituting u = 1 – y² back here,
-(1 – y²)1/2 + C = ∫ sin x dx
Substitute y = sin x back here,
-(1 – sin²x)1/2 + C = ∫ sin x dx
-(cos²x)1/2 + C = ∫ sin x dx
-cos x + C = ∫ sin x dx
Hence proved.
Definite Integral of Sin x
We know that ∫ sin x dx = -cos x + C. So according to the fundamental theorem of calculus, ∫ₐᵇ sin x dx = [-cos b + C] – [-cos a + C] = -cos b + C + cos a – C = -cos b + cos a. Therefore, the integration constant C plays no role when determining sin x’s derivative. Let us see some examples.
Integral of Sin x From 0 to π
∫₀π sin x dx = [-cos x]₀π
= -cos π – (-cos 0)
= -(-1) + 1
= 2
Thus, the integral of sin x from 0 to π is 2.
Integral of Sin x From 0 to π/2
∫₀π/2 sin x dx = [-cos x]₀π/2
= -cos π/2 – (-cos 0)
= -(0) + 1
= 1
Thus, the integral of sin x from 0 to π/2 is 1.
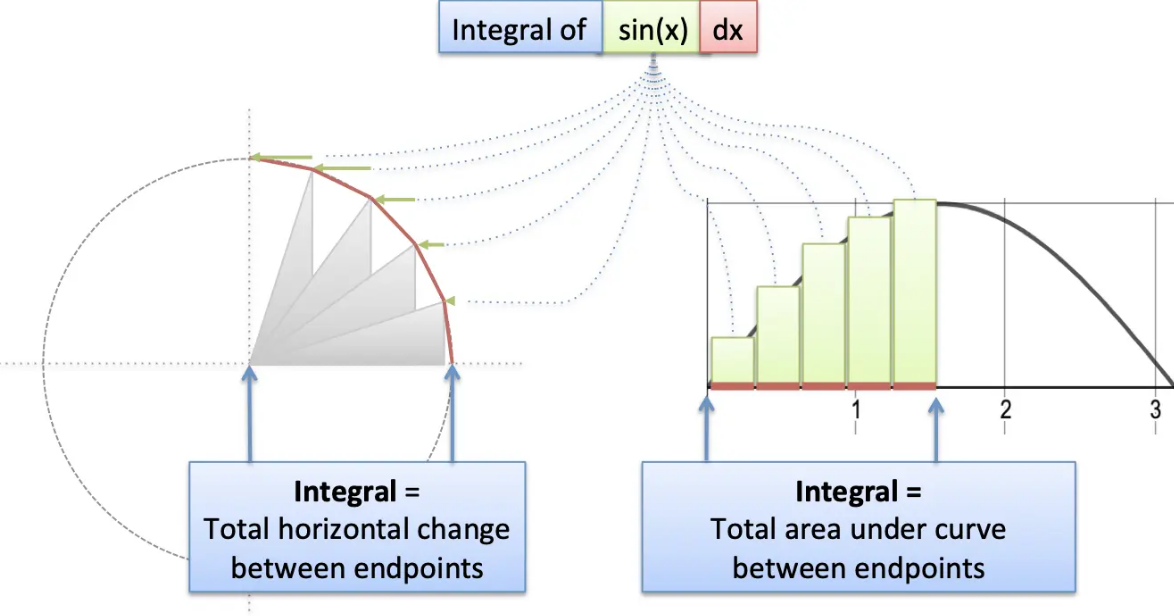
Integral of Sin x Graphical Intuition
An integral of a function within an interval is the area occupied by the graph of the function within the interval. Let’s plot the function f(x) = sin x and calculate the approximate area under the curve for some intervals using basic geometric formulas. Using the definite integration of sin x within the same intervals, let’s also calculate the exact areas. Let us compare both the results.
Let us calculate the areas under the curve in each interval [0, π/2] and [0, π]. These areas can be approximated by drawing triangles. However, this is not a reliable method. From the figure, the area calculated is less than the actual area as the triangle(s) doesn’t cover the complete area under the curve.
The numbers in the second column and the third column are approximately equal (of course, the numbers in the second column are lower than those in the third column since the triangles do not cover the entire area). As a result, the integral of sin x is -cos x and can be proved geometrically.